4 novembre 2015

Le lean et le supply chain management cherchent à réduire la variabilité dans la supply chain, permettant un fonctionnement plus efficace, plus fluide, plus agile. En dépit de ces efforts, si la variabilité peut être réduire, elle ne peut que rarement être totalement éliminée, ne serait-ce que pour prendre en compte la variabilité de la demande client.

Aussi, un positionnement de stocks, et notamment de stocks de sécurité, est-il toujours nécessaire dans certains cas, pour être en mesure de répondre sous un délai court à des demandes clients. Le stock de sécurité est destiné à couvrir la variabilité des demandes. Je propose que nous nous attachions à la façon de les déterminer.

Cet article en 3 parties sur les « stocks de sécurité » dans la supply chain traitera successivement :

• 1^ère partie : Analyse critique de la formule
• 2^ème partie : Quel dimensionnement ?
• 3^ème partie : Quelques points d’approfondissement

1^ère partie : Analyse critique de la formule

Introduction : Importance du stock de sécurité

Deux composantes du stock sont habituellement calculées : le stock de sécurité d’une part et le stock tournant d’autre part.

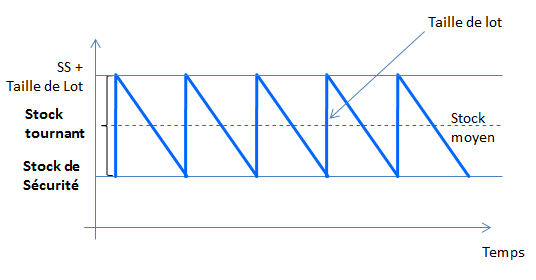
Le stock est cependant constitué de plusieurs autres composantes dont :

• Un stock d’anticipation, pour couvrir une période pendant laquelle aucun approvisionnement ne sera possible, ou pour constituer progressivement un stock avant une période de forte demande,
• Un stock d’opportunité consistant à constituer du stock lorsque les prix sont bas. Ceci concerne des produits dont les prix fluctuent significativement ou peut concerner des produits aux prix stables juste avant une augmentation de tarif,
• Un stock « Last Time Buy » destiné à couvrir la fin de vie d’un produit lorsque le fournisseur décide de l’arrêt d’une production. Ce stock n’est acquis que s’il y a une justification économique ou en termes de service de l’acquisition de ce stock,
• Des surstocks éventuels, si aucune des raisons précédentes n’explique la constitution de ce stock,
• Des en-cours correspondant à des quantités en cours de service ou en cours de mise en stock suite à une réception fournisseur,
• Des retards ou des avances de livraison du fournisseur.

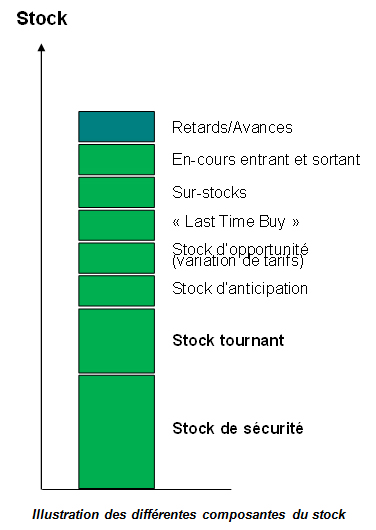
Le stock de sécurité représente cependant une part prépondérante de ce stock, dans un environnement de distribution :

• Sur les références de classe A, les stocks de sécurité auront une part prédominante, généralement supérieure à 70%, car la rotation importante des stocks, les fréquences d’approvisionnement élevées et les tailles de lot réduites permettent de limiter le stock tournant,
• Sur les références de classe C, le stock de sécurité représente moins de 25% du stock,

Au global, le stock de sécurité représente souvent 50% du stock total, voire nettement davantage dans des activités avec des flux très réduits, telles que des activités de pièces de rechange.

L’étude des stocks de sécurité se justifie donc d’une part pour une raison économique, le stock de sécurité représentant une part très significative du stock et d’autre part parce qu’il conditionne la qualité de service aux clients.

Partie 1 : Analyse critique de la formule incontournable

1. La formule de base et son explication 

La formule classique du Stock de Sécurité :

C’est à la fois une formule ancienne, datant des années 1930 où Wilson préconisait l’approvisionnement de quantité économique (selon la formule qui porte son nom) combiné avec un point de commande qui intègre un stock de sécurité selon une formule très proche de celle mentionnée ci-dessus^a.

Comment interpréter cette formule ?

Le stock de sécurité est dimensionné pour faire face aux aléas de la demande sur un cycle de réapprovisionnement:

- Sigma correspond à l’écart-type de la prévision, c’est-à-dire la précision de la prévision. Dans la plupart des logiciels, c’est l’écart moyen absolu (EMA) ou Mean Absolute Deviation (MAD) qui est déterminée. Lorsque la demande suit une loi normale  sigma = 1,25xMAD, ce qui permet d’ajuster la formule précédente

 

- Délai + Périodicité correspond à un cycle de réapprovisionnement composé du délai de livraison à partir de la passation de commande et de la périodicité de commande :

• Dans le cas d’une gestion par point de commande, seul le délai de livraison est pris en compte, car la commande pouvant être passée n’importe quand sans avoir à attendre d’échéance (même si en réalité, la détection ou le traitement des références ayant atteint le point de commande n’est généralement traité qu’une fois par jour, ce qui impliquerait une périodicité d’une journée),

• Dans le cas d’une gestion selon une périodicité de commande, le stock de sécurité doit couvrir le délai de livraison mais aussi une période d’approvisionnement.

- k correspond au coefficient de sécurité, le risque d’être en rupture pendant un cycle d’approvisionnement étant d’autant plus faible que la valeur de k est élevée.

Propriété remarquable de cette formule : dans l’hypothèse où la demande peut être modélisée selon une loi normale, et quelles que soient les valeurs du Délai, de la Période et de sigma , la valeur de k détermine la probabilité qu’une rupture se produise pendant un cycle de réapprovisionnement.

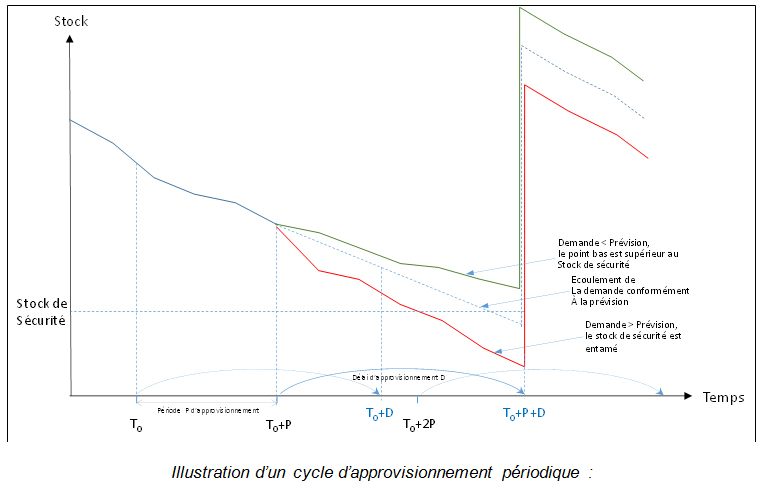
L’approvisionnement n’étant pas lancé en T₀ car, en projection, le stock de sécurité ne serait pas entamé en T₀+D. L’approvisionnement est lancé en T₀+P car le stock prévu à réception de la commande (T₀+P+D) entame le stock de sécurité. Le stock de sécurité doit de ce fait permettre de couvrir les aléas de demande pendant le délai d’approvisionnement D mais également pendant la période de commande P : en ne commandant pas T₀, mais à la période suivante,  le stock de sécurité doit couvrir les aléas de la demande entre T₀ et T₀+P+D.

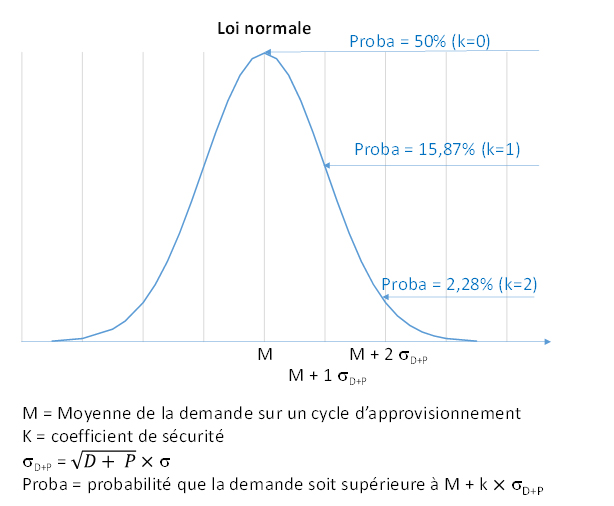
Illustration de la loi normale qu’est supposée suivre la demande, ainsi que la probabilité de rupture en fonction de quelques valeurs de k, c’est-à-dire en fonction de l’importance du stock de sécurité

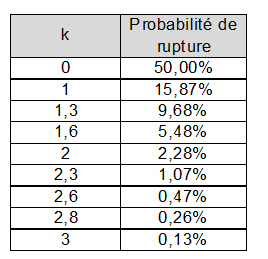
Cela paraît finalement élémentaire, mais cela n’empêche pas de nombreux contresens et des approximations.

En premier lieu, dans certains cas, la formule appliquée omet le paramètre Périodicité^a, ce qui conduira à minorer le stock de sécurité si la Périodicité est significative.

D’autres approximations sont rencontrées telles que « le stock de sécurité dépend du taux de service que vous avez spécifié […] ainsi que la précision de la prévision ». Il s’agit en fait d’un contresens, en cofondant taux de service et probabilité de rupture, ce qui, en termes statistiques, correspond à confondre une probabilité et une espérance mathématique.

Mais la probabilité de rupture est une information peu parlante, décalée avec le niveau de service qui correspond à un réel indicateur de performance. Aussi, la vraie question est de déterminer quel est le lien entre taux de service et le niveau du stock de sécurité…

2. Lien entre le taux de service et la probabilité de rupture

2.1  Détermination du taux de service sur un cycle de réapprovisionnement

Nous prenons toujours l’hypothèse dans cette étude que seule la demande présente de la variabilité.

Toujours en supposant l’application de la loi normale, on peut établir le nombre de ruptures potentielles sur un cycle d’approvisionnement : il s’exprime en pourcentage de 

Le taux de rupture, c’est-à-dire le nombre de ruptures sur un cycle d’approvisionnement est un pourcentage des pièces non servies divisé par la demande moyenne sur ce cycle. Pour le déterminer, il suffit de multiplier la probabilité précédente par l’indice de dispersion^b qui se calcule comme

En considérant la référence R₁, dont la prévision est très précise (ID = 0,10) et un coefficient de sécurité de 0, la probabilité de rupture est de 50% mais le taux de rupture n’est que de 4% (c’est-à-dire un taux de service de 96%). A l’inverse, la référence R₄, avec une forte dispersion de la demande (ID = 0,50), a un taux de rupture de 20% (c’est-à-dire un taux de service de 80%) avec un coefficient de sécurité k=0.

De façon générale, pour une même valeur de k, le taux de rupture sera d’autant plus élevé que l’indice de dispersion est élevé, c’est-à-dire que la demande présente une forte variabilité.

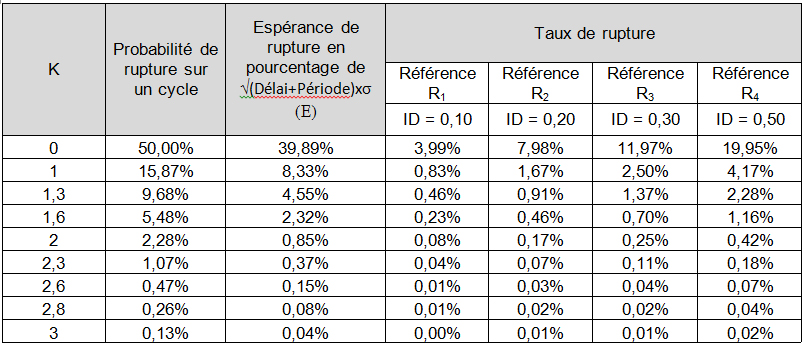
Illustration des probabilités et rupture et taux de rupture pour plusieurs valeurs de k et de ID

2.2 Détermination du taux de service annuel

Le taux de service moyen annuel d’une référence dépend en particulier du taux de service pendant un cycle d’approvisionnement mais aussi du nombre d’approvisionnements réalisés par an. Par exemple, une référence A₁ ayant un taux de service pendant un cycle d’approvisionnement de 98,3%, un Délai + Périodicité de 3 semaines, et commandée une fois par an aura un taux de service de 100% -(1,8%*3/52) = 99,9%

Une référence A₂ approvisionnée douze fois par an aura un taux de service moyen de 100%-(1,8%*3/52*12) = 98,8% sur l’année

Enfin, une référence approvisionnée généralement toutes les semaines (48 approvisionnements par an), aura un taux de service moyen de 100%-(1,8%*3/52*48) = 95,0%

En synthèse, le taux de service annuel dépendra très fortement de la fréquence à laquelle des commandes sont effectivement passées

2.3  Les limites de la formule du stock de sécurité

La formule, nous l’avons vu, est facile à mettre en œuvre.

En revanche, le taux de service moyen de la référence dépendra très fortement des paramètres suivants :

• Le coefficient de sécurité k, bien sûr,
• L’importance de la variabilité de la demande sur un cycle d’approvisionnement (Indice de dispersion)
• La fréquence effective des approvisionnements (espacement moyen des commandes effectivement passées)
• Le délai de livraison + la périodicité de commande (espacement des dates auxquelles on est autorisé à passer commande)

Or il est difficile voire impossible de positionner et d’ajuster régulièrement sur chaque référence une valeur k adaptée aux objectifs de taux de service en fonction des deux derniers paramètres.

De plus, dans les calculs précédents, plusieurs facteurs influants ont été omis :

• Le délai de livraison est considéré comme fixe, ce qui revient à considérer un taux de service fournisseurs de 100%, ce qui correspond rarement à la réalité. La fréquence et de l’amplitude des retards de livraison (délai réel > délai théorique) est un  facteur qu’il faudrait aussi intégrer dans les modélisations précédentes.
• Plus rarement, d’autres aléas internes peuvent être à considérer, par exemple la qualité de la tenue des stocks (écarts entre les stocks physiques et informatiques) ou des aléas sur les processus de réception et de mise en stock.
• Enfin, le modèle précédent suppose l’application d’une loi normale. Or ce n’est pas la loi universelle : en cas de demande faible, d’autres lois de probabilité peuvent s’appliquer comme la loi de Poisson ou la loi binomiale négative. La prise en compte d’une hypothèse de loi normale risque de conduire à sous-dimensionner le stock de sécurité requis pour garantir un niveau de service donnée.

Bref, la formule précédente est-elle à rejeter, ne fait-elle plus sens aujourd’hui ?

La 2^ème partie du Billet de Thierry Bur N°10 « Stocks de sécurité dans la supply chain : quel dimensionnement ? » sera mise en ligne le 18 novembre 2015

 

Notes :

Tags : agilité, Distribution Requirements Planning, DRP, gestion des approvisionnements, gestion des stocks, Inventory Management, Just In Time, Lean Manufacturing, Material Requirements Planning, MRP, multi-echelon inventory optimization, relation fournisseur, safety stock, stock de sécurité, stock tampon, supplier relationship management, Supply Chain Management, variabilité des processus